
全國咨詢熱線13817443004
熱門新聞ot news
聯(lián)系我們ontact

地址:上海市松江漢橋文化科技園B座703

咨詢熱線:13817443004

微信公眾號
E01,通過(式(76)-(80))進行修正,而作為E07標注的方法使用(式(88))而不是( 式(76))。然后,可以利用固有參數的平移值來模擬目標條件下新的I-V曲線。
E02:血清法
Z初,我們有(方程(92)-(94))利用了SC、OC和MPP點。此外,由于平行電阻Rsh, 未知數減少到41使用在SC處計算的dI /dV的倒數進行近似(公式(97)):
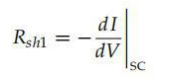
因此,只需要一個方程來求解系統(tǒng)。已知P = I·V對V的導數在MPP處必須為零,這樣就可以推 導出以下表達式(式(98)):
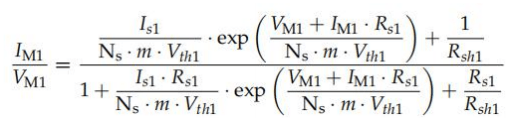
一旦參數,就可以使用平移方程,模擬任何目標條件下的曲線。塞拉等人。[60]建議使用
(公式(85))代替(公式(77))進行校正是.要轉換Iph,方法E02可使用(式(99)),而方 法E08使用(式(100)):
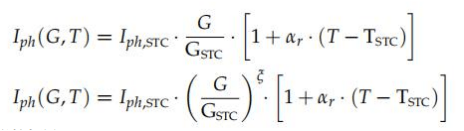
E03:東方巖的方法
為了將未知數減少到3個,Orioli和Di Gangi [61]假設Iph等于ISC在相同條件下(等式( 101)): Iph1=ISC1(101) 這組方程由(方程(96))和兩個新的附加方程(方程(102)和(103))組成,這樣的未 知數為(Is1, m,接收站1):
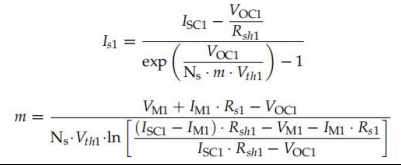
一旦確定了未知數,這種方法將使用不同的程序來轉換飽和電流是.首先,我們假設接收站2= 接收站1和Rsh2=Rsh1.然后第2版使用(式(43))進行計算。Z后,得到了新的值是2是由 (方程(104)):
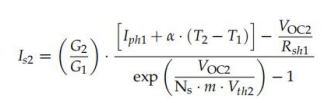
此方法E09與E03相同,但使用(式(88))而不是(式(76))來進行校正Iph.
E04:DeSoto的方法
德索托等人。[62]提供了一些平移方程來修正STCs的固有參數到其他輻照度和溫度的條件 (見(式(106)),二極管理想因子m沒有除以Eg如在之前的其他表達式中,要翻譯的是):
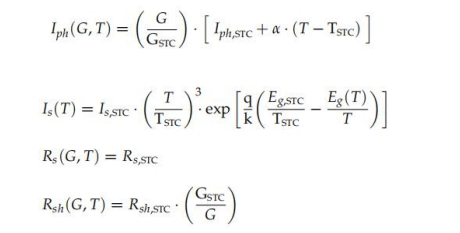
該方程組由(方程式(92)-(94)和(98))組成,要求解決一個額外的條件。利用平移 方程,可以表示Iph(T2)、Is(T2)和職業(yè)(T2)Iph1,是1和第1版,通過(式(109))-( 111)):
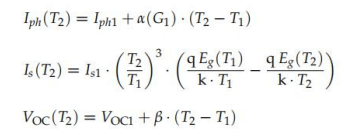
因此,在工作溫度下,使用OC點可以實現(xiàn)第五個方程T2(式(112)),并假設Rsh (T2) = Rsh1:
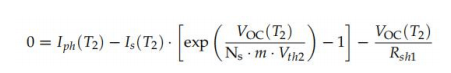
另一種可能性是使用(公式(88))來翻譯Iph,這的過程在本文中稱為E10。
E05:托萊多方法
這種由Toledo和Blanes [63]開發(fā)的方法需要從初始曲線中輸入四個任意的I-V點作為輸入 來提取SDM的參數。因此,對于每個點,我們都需要電壓坐標Vj、當前坐標Ij,以及在該點上的 I-V曲線的斜率。在我們的論文中,該方法使用SC、OC、MPP和MPP和OC之間的一個附加點進行了 測試,使用a-冪函數(在描述該方法的原始論文中定義)和= 10進行估計。 該方法是基于一個變量的單個方程的分辨率,稱為E。讓{V1,V2,V3,V4是四個選定點的電 壓坐標,I2,I3,I4這些點的當前坐標,以及{IIII}在這些點上關于V的斜率或導數。 首先, 以下函數{P1,P2,P3,P4}定義為:
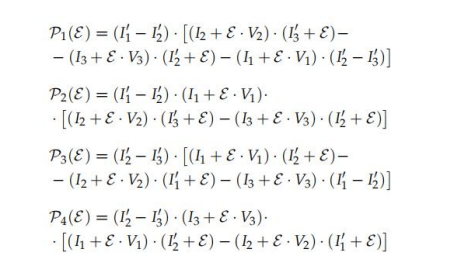
在第二步中,{Q1, Q2, Q3, Q4}還定義了:
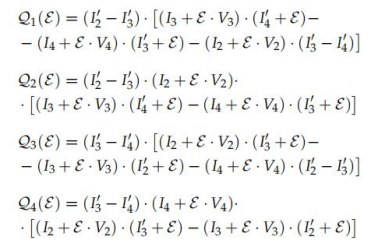
現(xiàn)在,可以定義多項式Z(E)(方程(121)):
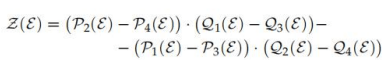
有必要找到一個小于任何{IIIII}的J對值的多項式的根。 這個值將等于輔助變量E。 然后,可以使用(方程(122)-(126))得到其他輔助變量K、D、C、B、A:
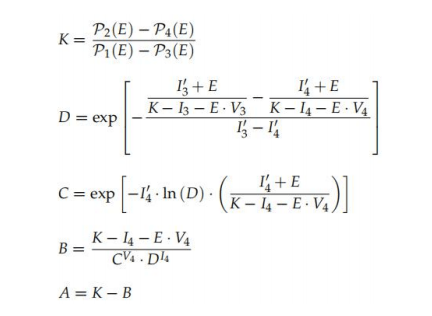
內在參數由(式(127)-(131))給出,假設在我們的論文中平行細胞的數量為Np= 1:
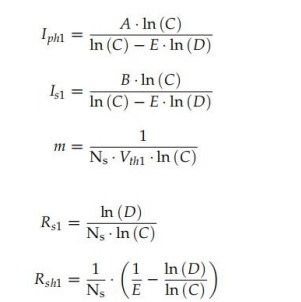
Z后,方法E05使用(公式(76)、(77)、(79)和(80))將這些參數轉換為G和T的其他 條件,并使用SDM(公式(9))對I-V曲線進行模擬。在方法E11的情況下,(式(76))用(式 (88))代替。
E06:肖的方法
為了減少SDM中未知參數的數量,該方法忽略了平行電阻,i。e. , Rsh! ¥ .另一個合理 的簡化方法是識別所生成的照片Iph1 電流與短路電流有關ISC1( Iph1=ISC1).因此,需要三個方 程組來求解這個方程組。D一個是MPP點下的SDM模型(式(132)):
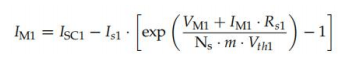
第二個方程可以是飽和電流is的表達式1作為二極管理想性因子m的函數:
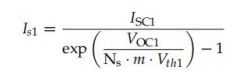
第三個方程來自于串聯(lián)電阻Rs的表達式1,根據理想性因子m(方程式(134)和(135)):
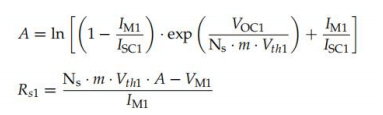
Z后一步是修正來自(G1,T1)至(G2,T2使用 (公式(76)、(77)、(79)和(80))。方法E12是相同的,但是使用了(式(88))而不 是(式(76))。