
全國咨詢熱線13817443004
熱門新聞ot news
聯系我們ontact

地址:上海市松江漢橋文化科技園B座703

咨詢熱線:13817443004

微信公眾號
摘要:光伏文獻包含了廣泛的方法,將太陽能器件的I-V曲線轉換為其他輻照度和電池溫度的條件,與進行測量的條件不同。其中一些翻譯方法被包括在國際標準IEC 60891的一部分中。本文對這些技術進行了分類、回顧和實施,并對它們進行了深入的比較分析,并討論了它們在不同輻照度和溫度情景下轉換光伏組件I-V曲線的適用性。從分析中可以看出,IEC 60891中提出的插值方法在應用于修正中小輻照度和溫度間隙時,獲得了準確的結果。如果不可能進行插值,并且對于較大的輻照度校正,則可以應用IEC 60891 中描述的其他程序。然而,某些基于單二極管模型或雙二極管模型的顯式方法可以克服該標準提出的Z著名的方法。
關鍵詞:ASTM E 1036標準;IEC 60891標準;I-V曲線校正;I-V曲線平移;I-V曲線插值;室外測量。標準試驗條件。
介紹
將光伏(PV)組件的電流-電壓(I-V)曲線轉換為準確可靠的入射輻照度G和電池溫度T的不同條件,原因有二。首先,有必要在測量值之間進行有意義的比較。例如,比較不同太陽能電池的性能或評估光伏組件的時間退化。對于這些比較,廣泛使用了一套參考測試條件,如 IEC 60904-3 [1]中定義的標準測試條件(STC)。當在戶外測量I-V曲線時,尤其需要這種轉換,因為在那里不可能使輻照度和溫度條件等于STCs。
第二種需要平移I-V曲線的情況是估計PV系統的能量產量。該任務要求估算不同運行條件下的效率。這些條件通常包括一個大范圍的輻照度和溫度值,其中I-V曲線是不可用的,需要從已知條件下的曲線計算。解決這個問題的一個可能的解決方案是對每個測量的I-V曲線應用一個校正數學程序,估計如果該曲線在不同的輻照度和溫度條件下測量,該曲線將是怎樣的。桑德斯特羅姆[2]在1967年出版了Z著名的翻譯方法,從那時起被廣泛使用,并在幾年后被納入國際標準IEC 60891 [3]作為程序1。
安德森[4]發表了一套新的方程來解決[2]中的一些不正確性,這種新方法在ASTME1036- 02[5]中采用了該方法。然而,同一標準的后一個版本,見ASTME1036-15(2019)[6],已經轉向推薦由Marion等人提出的雙線性插值方法。[7],這需要四條測量的I-V曲線作為輸入。在標 準的IEC 60891 [3]中,有一個程序(程序3),它也是基于一個插值方法,使用三條測量曲線。事實上,還有許多其他的方法來執行I-V曲線校正。選擇了Z著名的方法,并對它們進行了比較分析。
本文的其余部分有以下結構:第1.1節包含了修正程序的新分類,而第1.2節回顧了Z有趣的方法。在第2節中,我們介紹了正在研究的光伏組件,并描述了實驗結果。第3節分析了每種研究方法的所得結果。Z后,第4節給出了結論。
目前已經發表了許多相關文獻來實現這一目標的方法。e.,修正了太陽能器件在不同的輻照度和溫度條件下的I-V曲線。赫爾曼和維斯納[8]提出了這些方法的基本分類代數方法(基于每個離散點的轉移)和數值方法,這需要一個曲線擬合優化所有點的曲線來確定模型參數:光生成電流變化,暗飽和電流,二極管理想因子m,系列電阻Rs和并行電阻Rsh.后一種方法假設有一個潛在的等效電路,它可以是單二極管模型(SDM)或雙二極管模型(DDM)。
在這項工作中,考慮了一些其他類別的方法:解析方法是指曲線擬合被一個方程組代替,使用主要電參數作為輸入(而不是曲線的所有點);顯式方法,基于以前的方法,但計算負擔很低,因為他們提出了一系列簡單的顯式表達式來獲得內在參數;迭代方法,與以前的方法不同的是,一個或兩個參數不能明確確定,需要簡單快速的迭代調整;插值方法,基于幾條測量曲線的離散I-V點的插值來得到目標曲線。Z后,我們包括了另一類簡單的縮放方法,基于新條件下的電參數的初始計算,然后估計I-V曲線,通過縮放每個單獨的點的坐標到這些值:
A.縮放方法
在過去的幾十年里,許多研究論文和光伏手冊[9-13]提出了一組類似于(方程(1)和(2))的方程,允許短路電流的直接校正ISC和開路電壓職業從初始條件到目標條件。ISC2的值和第2 版對于新的條件(G2,T2)是直接使用一對簡單的方程來計算的ISC1和第1版在初始條件下的測量值(G1,T1);同時也通常會包含第三個方程來得到下午2點從…下午1點(方程(3))。一般來說
,這些公式需要預先知道主溫度系數的值和其他一些內部參數,如開路電壓的輻照度校正因子6
、二極管理想性因子m,或串聯電阻接收站.
其中,a、β、γ為,為的相對于細胞溫度的變化系數ISC, STC,VOC、STC和PM, STC,分別,通 常由制造商提供。

在應用(公式(1)和(2))之后,可以使用安德森[4,11]提出的并在(公式(4))中描述的簡單比例程序將初始曲線的每個I-V對修正到新的條件: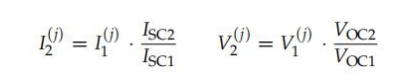
一旦得到完全修正后的I-V曲線,就可以估計修正后的值下午2點在尺度曲線上使用四次多項式回歸[14]。在這些方法中,提供了一個直接的公式來獲得下午2點,Z大功率的值可能在數值上與從縮放的I-V曲線中得到的值不同。在本文中,將考慮這兩種備選方案,提供來自比例曲線和直接公式的Z大功率的誤差。
B.代數方法
這組方法是基于對代數方程對初始曲線的每個離散樣本的應用,從而使坐標、電流和電壓位移到I-V平面的另一個點。第j個點的當前坐標使用(式(5))或(式(6))進行修改,而第二個方程類似 (公式(7))或(公式(8))用于改變電壓坐標。

如赫爾曼和維斯納[8]所述,基于方法(公式(5))或(公式(7))的缺點是通過移動原始曲線的點得到翻譯曲線,如果輻照度或溫度間隙很大,修正后的曲線可能沒有靠近軸的點。這意味著需要一個外推來估計ISC或職業,顯著增加了這些電參數的Z終誤差。
這些技術假定了一個描述被測設備行為的底層參數模型。一般來說,以往的文獻將SDM和 DDM作為等效電路[15]。兩者都建立了輸出電流和電壓之間的關系,其中存在一些未知的參數。擬合I-V曲線的第j個點應滿足這些隱式和非線性模型。在被稱為類型C的組中,我們希望總結基于SDM的方法,而那些使用DDM作為底層模型的方法則包含在類型D中。每個模型都有自己的參數,這樣就有必要找到一套值,使測量的和模擬的I-V曲線之間的誤差Z小化。對于SDM,這些參數是光產生電流Iph、暗飽和電流Is、二極管理想性/質量因子m、串聯電阻Rs和并聯/并聯電阻Rsh.SDM等效電路如圖1所示,而(式(9))描述了它的電行為:
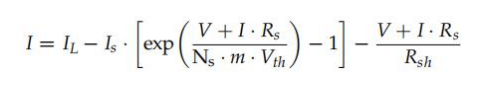
在哪里毫微秒是串聯細胞的數量,和Vth=k·T /q為熱電壓,分別為k = 1.380649 10 — 23J/K(玻爾茲曼常數)和q = 1.602176634 10 — 19C(基本電荷)。在這里,假設T在開爾文中表達。
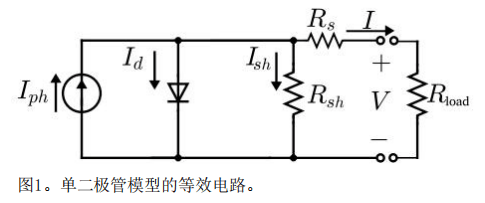
每個點(Vj)都必須滿足(式(9))中的表達式,Ij))的初始曲線,并得到的參數(Iph1,是 1, m1,接收站1,Rsh1)的假設是指一組條件(G1,T1).其中一些參數可以假定為器件的內部常數,但其他參數可以依賴于輻照度G1和/或細胞溫度T1.例如,可以在文獻[16-18]中找到匹配的表達式(等式(10)-(13)),以將變量參數從初始條件(G1、T1)到目標條件(G2,T2).通常這些公式需要事先知道一些額外的內在系數,如a(溫度系數ISC)或Eg(半導體材料的能帶隙),這可以是有利的由制造商提供的或每個光伏技術的通用值可以從文學。
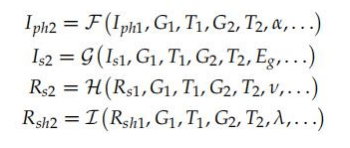
因此,由(公式(9))表示的模型可以使用任何數學套件中包含的曲線擬合程序進行調整,如Matlab [19],它以一個包含所有點(Vj)的矩陣作為輸入,Ij))并返回所需參數(Iph1, 是1, m,接收站1,Rsh1, ...)指的是初始條件(G1,T1).下一步是將這些條件下的參數轉化為目標條件(G2,T2通過(公式(10)到(13)的公式。Z后,有可能在輻照度下產生一個I-V曲線G2和溫度T2,定義一個電壓點網格,并將(式(9))中的每個坐標值替換,得到其當前圖像,Z終得到完整的模擬I-V曲線。
如果以DDM等效電路作為基礎模型,則可以采用與前一種方法類似的方法。在這種情況下,許多作者[20–23]假設一個表達式(公式(14)),使用兩個指數元素(見圖2),以這樣的方式,D一個二極管(與m1 = 1)考慮了在準中性區域的現象,而第二個二極管(與m2= 2)與空 間電荷區[24]中的載流子重組有關。
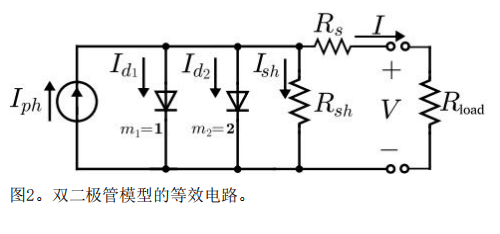
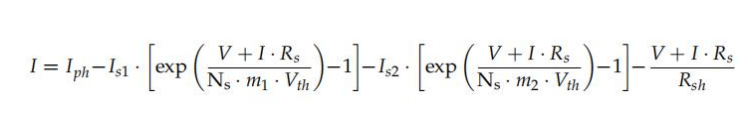
哪里有兩個暗飽和電流值是1 和是2 為了確定,是否有兩個不同的表達式用于轉換初始條件下的 值(G1,T1)到目標條件(G2,T2)(除了其他平移方程之外)。在其初始公式中,該模型有5個參 數需要估計,但一些作者提出了替代方法,其中m1and/or m2也是需要調整的自由參數。
這組的方法也基于太陽能電池的物理模型,目標是確定參數(Iph1,是1, m,接收站1,Rsh1, ...)指的是初始條件(G1,T1)和他們隨后的修正到(Iph2,是2, m,接收站2,Rsh2, ...)與目標 條件(G2、T2),Z后模擬了后一種條件下的I-V曲線(假設m是一個恒定的內在參數)。然而, 優化程序不是使用I-V曲線的所有離散點作為輸入,而是使用主要電參數的值和曲線在某些特 定點的斜率作為輸入。 基礎模型(對I-V曲線的所有點都有效)是針對一些特殊條件進行實例化的。這樣,就有 可能獲得僅在“短路”點有效的特定表達式(取決于所需參數),而另一個表達式僅適用于“ 開路”條件,以此類推。Z后,需要得到一個等于自由參數數的方程組,才能得到一個具有唯 一解的方程組。由于這些方程將是非線性的,因此有必要使用復雜的系統求解器例程,這需要 大量的硬件資源。 一旦方程組被求解,初始條件的參數(G1,T1)被修正到目標條件(G2,T2),Z后可以重建 在這些條件下的I-V曲線。與C型或D型方法的根本區別是,沒有必要適合所有的初始我曲線的 基礎模型來確定參數,但他們只從主要電氣參數,也許從一些其他的值可以估計我曲線。
F.顯式方法
與前一組相同,該類型還包括一些基于在初始條件下測量的I-V的主要電參數的方法。然 而,為了避免求解非線性方程組,應用了一些合理的假設來執行各種代數操作,Z后獲得一系 列用于確定所有所需參數的顯式表達式,需要較低的計算負擔[25–27]。Batzelis [28]對這些 顯式方法進行了綜述。 一旦確定了所需的參數并修正到目標條件,基礎模型將用于重建新的測量條件下的曲線。 在這類方法中,通常使用快速替代方法來重建I-V曲線,而不是使用通用的非顯式模型。例如, 可以通過W-蘭伯特函數[26]對(式(9))中定義的基礎模型進行重新表述,這樣每個電流坐標都 可以從前面確定的電壓坐標的值和前面確定的其他參數中明確地得到。
G.迭代方法
與前一種類型類似,底層模型所需的大多數參數都可以使用主要電參數的顯式表達式來估計。然而,一個參數(或其中的幾個)必須通過一個簡單而快速的迭代例程來確定,當模擬曲線滿足一個預定義的準則時,該例程將完成。或者,在某些方法中,必須預先知道一些要確定的參數,因此應該預先執行一種只確定該參數的方法。
H.插值方法
在前幾類方法中,在Z終條件下,只使用一個W一的初始I-V曲線作為輸入來生成目標I-V 曲線。另一方面,H型方法允許結合一些參照條件的初始曲線(G1a, T1a), ( G 1 b, T1b),. . . ,以獲得與目標輻照度和溫度相關聯的輸出曲線(G2,T2).
在這種方法中,通過對作為輸入的初始曲線的不同點進行插值,得到了新的I-V曲線。其中一個缺點是,這些插值方法不能應用于每一組初始曲線。有必要找到一個滿足一定準則的初始曲線的組合。當目標條件超過初始條件定義的間隔時,可能會出現另一個缺點。在這些情況下,它不是一個插值,而是實際上是一個外推,這可能導致高誤差[29,30]。